二叉树
二叉树
基本定义
二叉树(binary tree)是一种非线性数据结构,代表“祖先”与“后代”之间的派生关系,体现了“一分为二”的分治逻辑。与链表类似,二叉树的基本单元是节点,每个节点包含值、左子节点引用和右子节点引用。

类型
- 平衡二叉树(balanced binary tree)中任意节点的左子树和右子树的高度之差的绝对值不超过 1 。
- 完美二叉树(perfect binary tree)所有层的节点都被完全填满。
- 完全二叉树(complete binary tree)只有最底层的节点未被填满,且最底层节点尽量靠左填充。
- 完满二叉树(full binary tree)除了叶节点之外,其余所有节点都有两个子节点。
遍历
遍历方法:
- 深度优先:先序遍历、中序遍历、后序遍历。
- 广度优先:层序遍历。
/* 前序遍历 */
void preOrder(TreeNode *root) {
if (root == nullptr)
return;
// 访问优先级:根节点 -> 左子树 -> 右子树
vec.push_back(root->val);
preOrder(root->left);
preOrder(root->right);
}
/* 中序遍历 */
void inOrder(TreeNode *root) {
if (root == nullptr)
return;
// 访问优先级:左子树 -> 根节点 -> 右子树
inOrder(root->left);
vec.push_back(root->val);
inOrder(root->right);
}
/* 后序遍历 */
void postOrder(TreeNode *root) {
if (root == nullptr)
return;
// 访问优先级:左子树 -> 右子树 -> 根节点
postOrder(root->left);
postOrder(root->right);
vec.push_back(root->val);
}
/* 层序遍历 */
vector<int> levelOrder(TreeNode *root) {
// 初始化队列,加入根节点
queue<TreeNode *> queue;
queue.push(root);
// 初始化一个列表,用于保存遍历序列
vector<int> vec;
while (!queue.empty()) {
TreeNode *node = queue.front();
queue.pop(); // 队列出队
vec.push_back(node->val); // 保存节点值
if (node->left != nullptr)
queue.push(node->left); // 左子节点入队
if (node->right != nullptr)
queue.push(node->right); // 右子节点入队
}
return vec;
}
二叉搜索树
定义
如下图所示,二叉搜索树(binary search tree)满足以下条件。
- 对于根节点,左子树中所有节点的值<根节点的值<右子树中所有节点的值。
- 任意节点的左、右子树也是二叉搜索树,即同样满足条件 1. 。
搜索
给定目标节点值 num ,可以根据二叉搜索树的性质来查找。如图 7-17 所示,我们声明一个节点 cur ,从二叉树的根节点 root 出发,循环比较节点值 cur.val 和 num 之间的大小关系。
- 若 cur.val < num ,说明目标节点在 cur 的右子树中,因此执行 cur = cur.right 。
- 若 cur.val > num ,说明目标节点在 cur 的左子树中,因此执行 cur = cur.left 。
- 若 cur.val = num ,说明找到目标节点,跳出循环并返回该节点。
插入与删除
搜索速度快,相应的插入和删除就会麻烦一些(因为要满足二叉搜索树的规范)
插入
二叉搜索树不允许存在重复节点,否则将违反其定义。因此,若待插入节点在树中已存在,则不执行插入,直接返回。插入的节点一定在最顶层,作为叶子节点。
为了实现插入节点,我们需要借助节点 pre 保存上一轮循环的节点。这样在遍历至 None 时,我们可以获取到其父节点,从而完成节点插入操作。
/* 插入节点 */
void insert(int num) {
// 若树为空,则初始化根节点
if (root == nullptr) {
root = new TreeNode(num);
return;
}
TreeNode *cur = root, *pre = nullptr;
// 循环查找,越过叶节点后跳出
while (cur != nullptr) {
// 找到重复节点,直接返回
if (cur->val == num)
return;
pre = cur;
// 插入位置在 cur 的右子树中
if (cur->val < num)
cur = cur->right;
// 插入位置在 cur 的左子树中
else
cur = cur->left;
}
// 插入节点
TreeNode *node = new TreeNode(num);
if (pre->val < num)
pre->right = node;
else
pre->left = node;
}
删除
前置知识:
那么我们知道,二叉搜索树是左<中<右,正好与中序遍历的遍历顺序一致。因此,如果按照中序遍历的顺序遍历二叉搜索树,就可以把所有节点值按顺序排列,从而得出一个重要性质:二叉搜索树的中序遍历序列是升序的。
比较复杂,根据目标节点的子节点数量,分 0、1 和 2 三种情况,执行对应的删除节点操作。
- 当待删除节点的度为0时,表示该节点是叶节点,可以直接删除。
- 当待删除节点的度为1时,将待删除节点替换为其子节点即可。
- 当待删除节点的度为2时,情况比较复杂,理论上应该按照顺序找出整个树里面按从小到大顺序排序的下一个节点来替换他,那后面的都要依次(递归)替换。这个数就是Node->right->left->left......这样子找到的节点就是中序遍历的下一个节点,然后删除(这个地方会形成递归) 它,直到完成递归。
AVL树
在多次插入和删除操作后,二叉搜索树可能退化为链表。在这种情况下,所有操作的时间复杂度将从O(logn)劣化为
O(n)。

AVL 树可以确保在持续添加和删除节点后,AVL 树不会退化,依然是平衡二叉树。AVL 树既是二叉搜索树,也是平衡二叉树,同时满足这两类二叉树的所有性质,因此是一种平衡二叉搜索树。
定义
/* AVL 树节点类 */
struct TreeNode {
int val{}; // 节点值
int height = 0; // 节点高度
TreeNode *left{}; // 左子节点
TreeNode *right{}; // 右子节点
TreeNode() = default;
explicit TreeNode(int x) : val(x){}
};
相关概念
- “节点高度”是指从该节点到它的最远叶节点的距离,即所经过的“边”的数量。叶节点的高度为0 ,而空节点的高度为-1。
- 节点平衡因子:节点左子树的高度减去右子树的高度,同时规定空节点的平衡因子为0。平衡因子>1就是失衡节点。
旋转
在失衡节点处做一个旋转操作即可让这个树恢复平衡。
如图这种情况就可以通过一次**右旋**操作完成平衡。
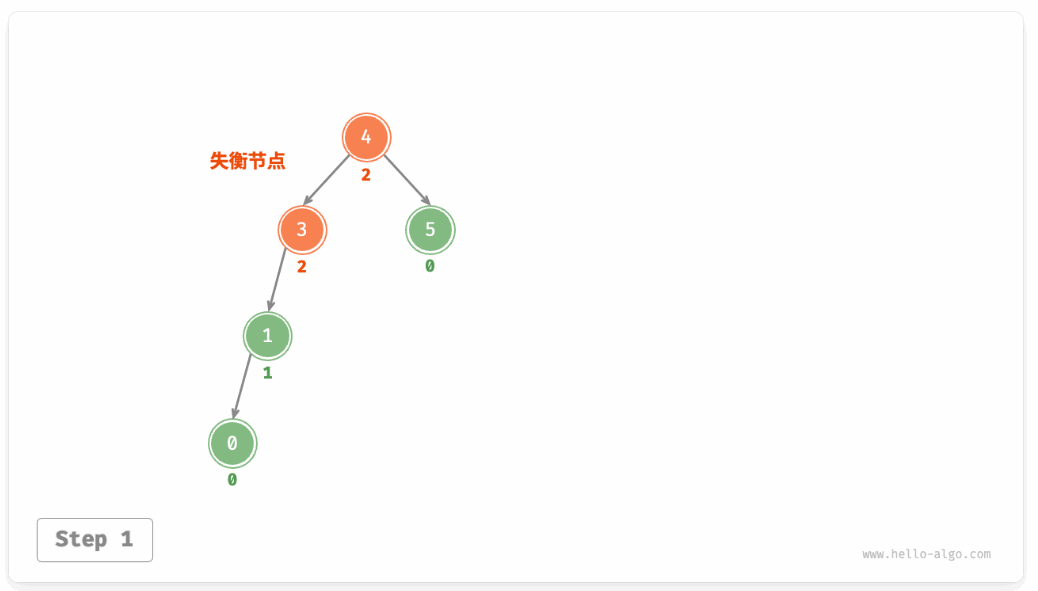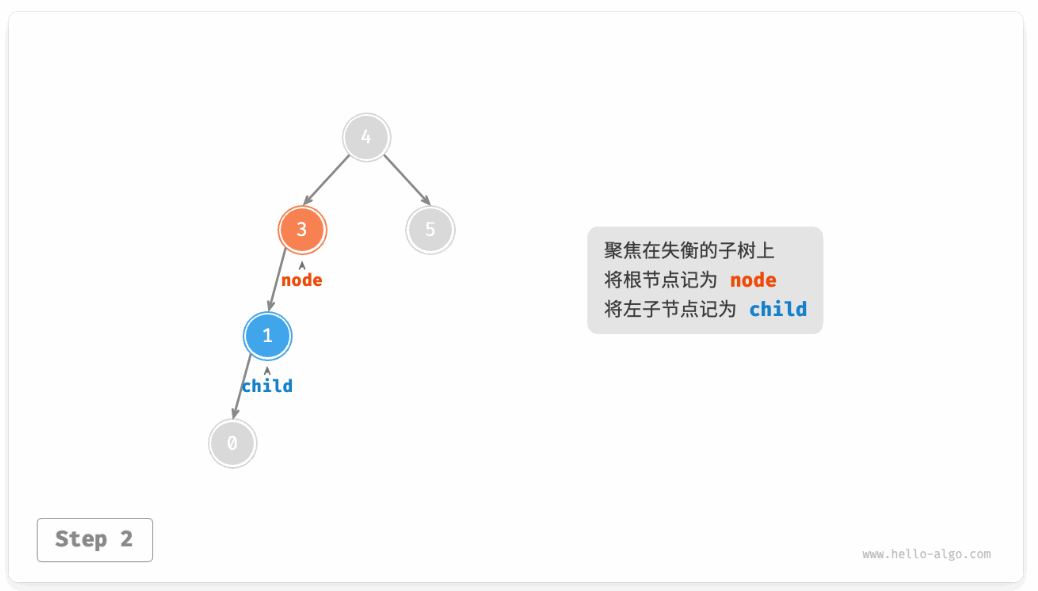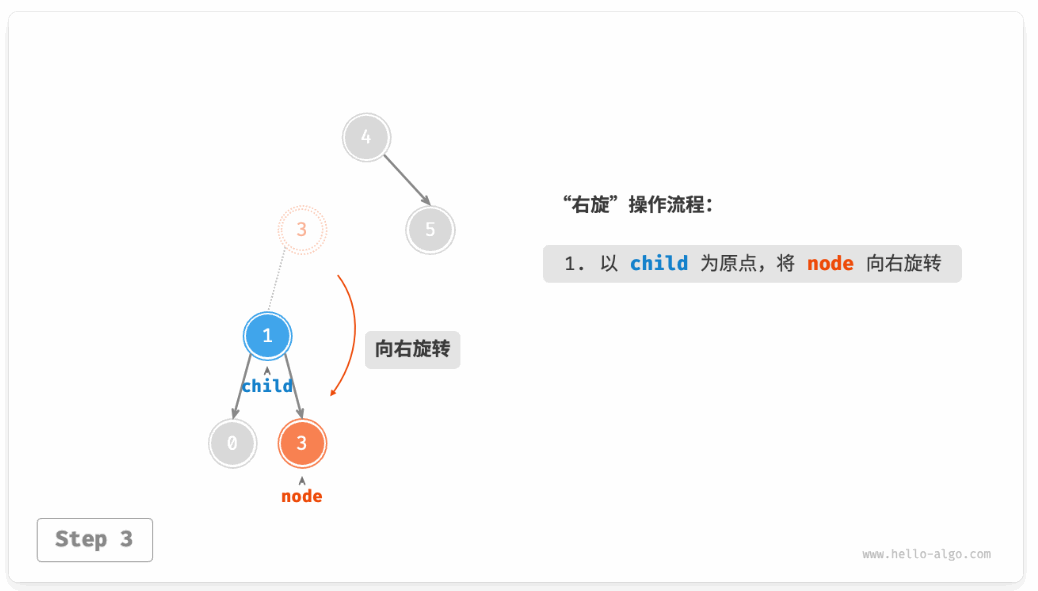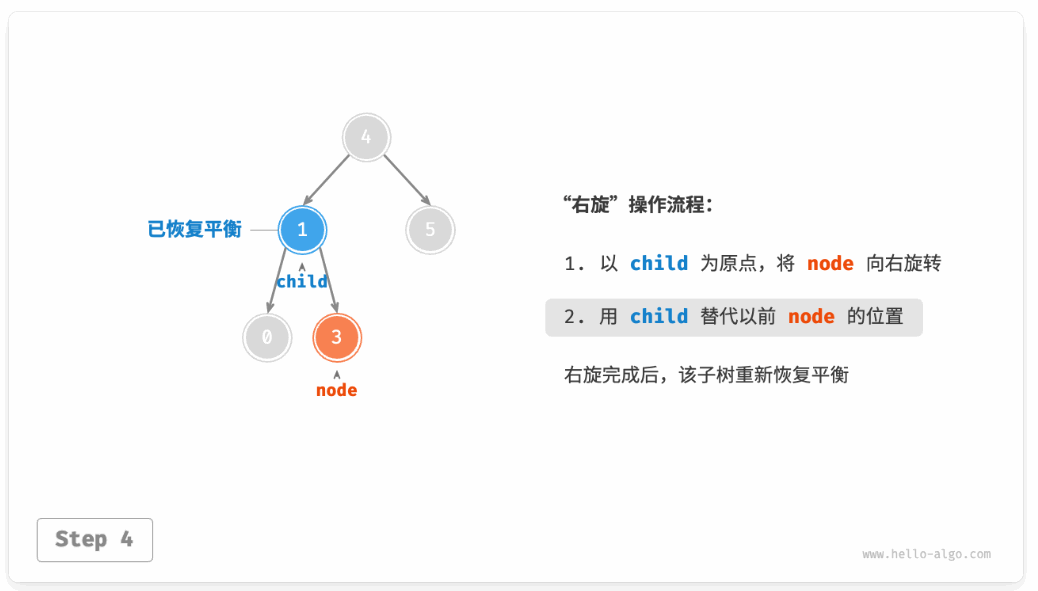
如图 7-27 所示,当节点 child 有右子节点(记为 grand_child )时,需要在右旋中添加一步:将 grand_child 作为 node 的左子节点。

同理,还有**左旋、右旋再左旋、左旋再右旋**。


旋转的选择:四种失衡情况与四种旋转方式逐个对应,分别需要采用右旋、先左旋后右旋、先右旋后左旋、左旋的操作。

感觉记一记形状就可以理解记忆,写代码的话得按这个表:
| 失衡节点的平衡因子 | 子节点的平衡因子 | 应采用的旋转方法 |
|---|---|---|
| >1 | >=0 | 右旋 |
| >1 | <0 | 先左旋再右旋 |
| <-1 | <=0 | 左旋 |
| <-1 | >0 | 先右旋再左旋 |
/* 执行旋转操作,使该子树重新恢复平衡 */
TreeNode *rotate(TreeNode *node) {
// 获取节点 node 的平衡因子
int _balanceFactor = balanceFactor(node);
// 左偏树
if (_balanceFactor > 1) {
if (balanceFactor(node->left) >= 0) {
// 右旋
return rightRotate(node);
} else {
// 先左旋后右旋
node->left = leftRotate(node->left);
return rightRotate(node);
}
}
// 右偏树
if (_balanceFactor < -1) {
if (balanceFactor(node->right) <= 0) {
// 左旋
return leftRotate(node);
} else {
// 先右旋后左旋
node->right = rightRotate(node->right);
return leftRotate(node);
}
}
// 平衡树,无须旋转,直接返回
return node;
}
插入和删除
AVL 树的节点插入操作与二叉搜索树在主体上类似。唯一的区别在于,在 AVL 树中插入节点后,从该节点到根节点的路径上可能会出现一系列失衡节点。因此,我们需要从这个节点开始,自底向上执行旋转操作,使所有失衡节点恢复平衡。
插入节点:
/* 插入节点 */
void insert(int val) {
root = insertHelper(root, val);
}
/* 递归插入节点(辅助方法) */
TreeNode *insertHelper(TreeNode *node, int val) {
if (node == nullptr)
return new TreeNode(val);
/* 1. 查找插入位置并插入节点 */
if (val < node->val)
node->left = insertHelper(node->left, val);
else if (val > node->val)
node->right = insertHelper(node->right, val);
else
return node; // 重复节点不插入,直接返回
updateHeight(node); // 更新节点高度
/* 2. 执行旋转操作,使该子树重新恢复平衡 */
node = rotate(node);
// 返回子树的根节点
return node;
}
删除节点:
/* 删除节点 */
void remove(int val) {
root = removeHelper(root, val);
}
/* 递归删除节点(辅助方法) */
TreeNode *removeHelper(TreeNode *node, int val) {
if (node == nullptr)
return nullptr;
/* 1. 查找节点并删除 */
if (val < node->val)
node->left = removeHelper(node->left, val);
else if (val > node->val)
node->right = removeHelper(node->right, val);
else {
if (node->left == nullptr || node->right == nullptr) {
TreeNode *child = node->left != nullptr ? node->left : node->right;
// 子节点数量 = 0 ,直接删除 node 并返回
if (child == nullptr) {
delete node;
return nullptr;
}
// 子节点数量 = 1 ,直接删除 node
else {
delete node;
node = child;
}
} else {
// 子节点数量 = 2 ,则将中序遍历的下个节点删除,并用该节点替换当前节点
TreeNode *temp = node->right;
while (temp->left != nullptr) {
temp = temp->left;
}
int tempVal = temp->val;
node->right = removeHelper(node->right, temp->val);
node->val = tempVal;
}
}
updateHeight(node); // 更新节点高度
/* 2. 执行旋转操作,使该子树重新恢复平衡 */
node = rotate(node);
// 返回子树的根节点
return node;
}
有什么用
- 组织和存储大型数据,适用于高频查找、低频增删的场景。
- 用于构建数据库中的索引系统。
- 红黑树也是一种常见的平衡二叉搜索树。相较于 AVL 树,红黑树的平衡条件更宽松,插入与删除节点所需的旋转操作更少,节点增删操作的平均效率更高。